


What's A Field?

|
|
Electric Fields
|
|
Merriam-Webster™ defines a field as a "region or space in which a given effect
exists".
For example, a
charged particle distorts its surrounding space in such a way that
another charged particle is either repelled or attracted, depending on whether
the charges have the same or the opposite polarity.
This electric force is directed along the straight line between the two
charges. Since the force has
both a value and a direction, it's a vector. The
mathematical symbol for a force vector is:
The standard unit of force is the newton, abbreviated N (capital N because Newton was a person).
The "region or space" wherein the electric force exists is the
electric field.
Electric Field Strength (E)
The electric field strength (symbol E)
at any point in an electric field is simply defined as the force (F) that a
unit of positive charge would feel
there, per unit of the field's source charge (q):
|
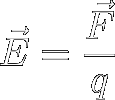
|
[1]
|
|
Like force,
E is a vector. The unit of charge (q)
is the coulomb (C) so the unit of electric field strength is the newton per coulomb (N ⁄ C).
An equivalent unit of field strength is the volt per meter—the
force of a one volt
potential between two parallel conductive plates that are one meter apart. One V ⁄ m is exactly one N ⁄ C.
1 V ⁄ m = 1 N ⁄ C
By convention, electric fields point in the direction that a positive
test charge would move—that is, away from positive
and toward negative charge:
Electric Field Lines

The field lines in the above illustration are a crude but helpful way
to picture a force field. The electric field strength is greater where the lines
are closer together. The direction of the field at any
particular point is tangent
to the field line.
Coulomb's Law
Charles-Augustin de Coulomb determined that the magnitude of the
electric force (FE) between
two charges (q1 & q2)
that are separated by a distance r is:
|
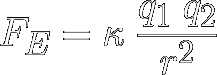
|
[2]
|
|
This equation looks like Newton's law of gravitational force—just
replace the two charges with two masses and put a different constant up front.
The electric constant is κ (kappa,
also called Coulomb's
constant). Kappa equals 1/4πε0
where
ε0 (epsilon zero) is the electric permittivity of free space
(its ability to permit an electric field).
Epsilon zero equals
1/μ0c2 where
μ0 (mu zero) is the magnetic permeability
of free space (its ability to hold a magnetic field) and
c is the speed of light.
|
|
Magnetic Fields
|
|
A magnetic field is generated whenever
charge
is in motion, either microscopically, like electrons spinning and
orbiting in an
atom,
or macroscopically, like electric
current
in a wire.
Bar Magnets
The magnetic field lines of a bar magnet are shown here.
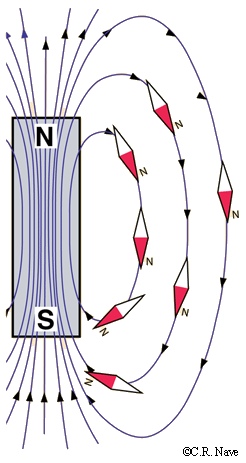
The magnetic force field arises from electrons in the bar, all spinning and
orbiting in the same direction.
One end of the bar is called the north pole and the other, the south.
Poles come in pairs and, by convention, the field lines point
from north to south.
As we can see from the magnetized compass needles in this drawing, opposite
poles attract. The north pole of each needle points toward the
south pole of the bar magnet.
The planet Earth has its own magnetic field. The field is generated by electric currents
resulting from the
convection of a molten mixture of iron and nickel in the Earth's outer
core. The convection is caused by heat escaping from the core.
Originally, a magnet's north pole was defined as the pole that is
attracted by Earth's "North Magnetic Pole". Now we know that
Earth's "North Magnetic Pole" must be the south pole of
Earth's magnetic field in order to attract the north pole of magnets.
Likewise, the Earth's "South Magnetic Pole" (where field
lines point downward into the Earth) is actually up near the North
Pole. Geomagnetic reversals do randomly occur, however, about 100 thousand to 50 million years
apart. The last reversal occurred about 780,000 years ago.
Current-Carrying Wires
The magnetic field around a
current-carrying wire is illustrated below. The yellow disc is
the cross section of a wire whose current
flows into the page ("X" represents the tail of an arrow).
The magnetic field lines curl around the current.
If you point your right thumb in the direction of the
current, your fingers will curl in the direction of the force field.
An opposite current produces an opposite curl.
NOTE : By convention, electric current flows from positive to
negative, opposite to the flow of electrons.
Unlike electric field lines, magnetic field lines have no beginning or
end—they're all closed loops. That's because the magnetic north and
south poles are a united dipole, unlike the separated plus and
minus electric charges called monopoles.
|
|
Electromagnetism
|
|
A moving charge not only creates a magnetic field but also
reacts to
one, including the one it created!
Electricity and magnetism are two tightly coupled aspects of a single electromagnetic
force that pulls on moving charges. The pull is
perpendicular to both the charge velocity (v) and
the strength of the surrounding magnetic field (B).
The illustration below shows the electromagnetic force (F)
acting on a positively charged particle that's moving perpendicular to
a magnetic field (B).
If you open your right hand and point its thumb in the direction of the
charge's velocity and point its fingers in the direction of the
magnetic field, then your palm will point in the direction of the
electromagnetic force.
Magnetic Flux Density (B)
At any point in a magnetic field, magnetic flux density (B) is
defined to be the electromagnetic force (F) that would be felt
there by a particular charge (q) moving
through the field at a particular velocity (v), per unit of
charge and
velocity.
Symbolically,
B = F/qv
Solving for F gives us :
F = qvB
However, one additional variable affects the electromagnetic force : the angle
between the charge's motion (v) and the direction of the magnetic field
(B).
To multiply two vectors (v and B)
having separate directions, a vector cross product is
required, written as
follows :
|
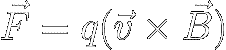
|
[3]
|
|
This cross product is a force F
whose direction is perpendicular to
both v and B
and whose magnitude takes into account the angle (θ, theta )
between v and B as follows :
|
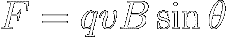
|
[4]
|
|
Where:
F = the electromagnetic force, in newtons
q = the electric charge, in coulombs
v = the charge velocity, in meters/second
B = the magnetic flux density, in teslas
θ = the angle between the velocity and the magnetic field
What's Flux?
As an analogy, consider a hollow tube held in a waterfall. If the
opening of the tube is perpendicular to the waterfall, the maximum
amount of water
will flow
through the opening.
But if the tube's opening is parallel to the waterfall, no water will
flow across it.
At in-between angles, an in-between amount of water will cross the opening.
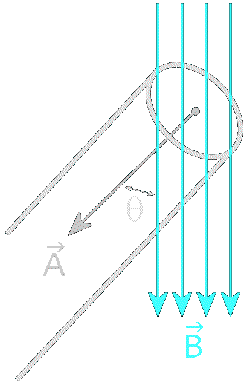
In this analogy, flux is the total amount of water
entering the tube at a particular moment.
The amount depends on the strength of
the waterfall, the angle it makes with the tube, and the area of the
tube's opening. In the same way, magnetic flux (capital Phi Φ)
is the portion of a magnetic field B
acting perpendicular to some surface area A.
This projection of B onto the
direction of
A is a vector dot product that returns
a scalar (non-vector) value as follows :
|

|
[5]
|
|
Where:
Φ = the magnetic flux, in webers
B = the magnetic flux density, in teslas
A = a surface area, in square meters
θ = the angle between the magnetic field and the surface area
Magnetic Units
The unit of magnetic flux (Φ)
is the weber, abbreviated Wb (capital W because Weber was a person).
The unit of magnetic flux density (B)
is the tesla, abbreviated T (capital T because Tesla was a person).
A subdivision of the tesla is the gauss, abbreviated G (capital G
because Gauss was a person). There are 10,000 gauss in a tesla.
1 T = 10 kG
Since Φ = B ⋅ A,
flux density (B) describes a flux per
area (Φ/A). That is, one tesla is
equivalent to one weber per square meter.
1 T = 1 Wb ⁄ m2
Although magnetic flux is mathematically convenient for calculating the
effects of a magnetic field, flux has no physical reality beyond the
mathematician's scratch pad.
In 1833, Wilhelm Weber and Carl Gauss built the first operative
telegraph. It ran between the Göttingen Observatory in
Germany and the Institute of Physics, about 1 km away.
Magnetic Field Strength (H)
In materials like iron, nickel and cobalt, electronic orbits and their
associated magnetic fields naturally align
with nearby magnetic fields, increasing the total flux density.
These materials are said to be magnetically permeable.
Magnetic field strength (symbol H)
is a raw field strength that does not include the effects of
magnetic permeability.
The unit of magnetic field strength is the ampere per meter (A / m),
which is the magnetic strength inside a coil of wire passing
one ampere of current per meter of coil length (not wire length).
In free space, to convert a raw field strength H
into a total flux density B,
the permeability of free space (μ0, mu zero:
the ability to hold
a magnetic field) must also be factored in :
B = μ0H
The factor μ0 is
a "dimensional" constant—that is, it has units.
Field strength (H) converts to flux
density (B) as follows:
1 A / m = 1.2567 microteslas = 0.012567 gauss
If a region's permeability isn't μ0,
another factor is needed to calculate B
from H. This dimensionless constant is
called the relative permeability (μr)
of the region, so that :
B = μrμ0H
Relative permeability is determined by experiment.
Lorentz Force Law
The Lorentz force law simply adds the magnetic force to the electric force.
The electric aspect comes from equation [1]:
|
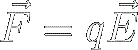
|
[1b] |
|
The magnetic aspect comes from equation [3]:
|
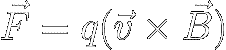
|
[3] |
|
The sum of these forces describes the total electromagnetic force on a charged
particle:
|
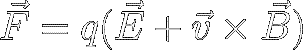
|
[6]
|
|
|
|
Field Theory
|
|
The previous equation, formulated by Hendrik Antoon Lorentz in
1895, embodies modern classical electromagnetism. In essence,
equation [6] is the definition of E
and B. They're the fields
needed to account for the force F.

The Lorentz force law is the culmination of the shift from the idea of
action at a distance—forces reaching out across empty
space without a mechanism or speed limit—to the idea of a field.
A "field" is the medium or mechanism that transmits stress
across a distance, from quantum to neighboring quantum at a finite
speed.
In physics, electromagnetism was the first field theory. The
electromagnetic
force is transmitted by virtual photons—quantum
fluctuations in the electromagnetic field.
|

|
|